Class Notes NCERT Solutions for CBSE Students
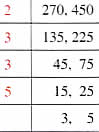
2. Common Division Method
Find the HCF of 270 and 450 using common division method.
Step 1. Divide the numbers by the lowest common prime number. Write the quotients below the numbers.
Step 2. Divide the quotients by the lowest common prime number.
Step 3. Stop when there are no common prime numbers to divide by.
HCF is the product of all the common prime factors.
HCF = 2×3×3×5 = 90
3. Long Division Method
(a) Find the HCF of 24 and 30 using the long division or the continued division method.
24) 30 ( 1
– 24_
last divisor →6) 24 ( 4
-24_
o _
HCF = 6
Step 1. Put the smaller number as the divisor.
Step 2. After dividing, the remainder becomes the divisor and the original divisor becomes the dividend.
Step 3. Continue this process till you get zero as the remainder.
Step 4. The last divisor is the HCF.
(b) Find the HCF of 532 and 905.
Always take the smaller number as the divisor.
532 ) 905 ( 1
-532
373 ) 532 ( 1
– 373
159 ) 373 ( 2
– 318
55 ) 159 ( 2
– 110
49 ) 55 ( 1
– 49
6 ) 49 ( 8
– 48
The last divisor 1 is the HCF → 1 ) 6 ( 6
– 6
0
HCF = 1
Step 1. Divide 905 by 532
Step 2. Reminder 373 becomes the new divisor and the previous divisor 532 becomes the dividend.
Step 3. Reminder 159 becomes the new divisor and the previous divisor 373 becomes the dividend.
Step 4. Reminder 55 becomes the new divisor and the previous divisor 159 becomes the dividend.
Step 5. Reminder 49 becomes the new divisor and the previous divisor 55 becomes the dividend.
Step 6. Reminder 6 becomes the new divisor and the previous divisor 49 becomes the dividend.
Step 7. Reminder 1 becomes the new divisor and the previous divisor 6 becomes the dividend.
Step 8. Reminder 0
Using HCF
(a) Find the greatest possible number that will divide both 63 and 48 and leave a reminder of 3. Find the HCF of these numbers after subtracting 3 from both the numbers.
63-3 = 60
48-3 = 45
HCF of 60 and 45 is 15.
Answer: 15 is the greatest possible number that can divide 63 and 48 leaving a reminder of 3.
