RECIPROCALS
Two numbers whose product is 1 are called reciprocals.
For example, 5/6 and 6/5 are reciprocals.
5/6×6/5 = 30/30 = 1
4 and 1/4 are reciprocals.
Step 1. Write the number as a fraction 7/1, 3/4, 5/2
Step 2. Interchange the numerator and denominator 1/7, 4/3, 2/5
DIVISION OF FRACTIONS
Dividing Fractions
To understand division of fractions let us look at division again.
If you had a sum 6÷2, you could think of it as ‘how many 2s are there in 6?’ The answer would be 3.
There are three 2s in 6.
Dividing a Whole Number by an Unit Fraction
(a) You can do the same thing when you divide by fractions.
To understand 3÷1/2, ask the question ‘how many halves in 3?’
These are three apples. Think: ‘how many halves in three apples?’
We can see that there are 6 halves in 3 apples.
3÷1/2 = 6
We can also describe the same picture as 3×2 = 6
Dividing by 1/2 is just like multiplying by 2.
Here is how you can solve the sum without pictures.
3 ÷ 1/2 = ?
Dividend Divisor
Step 1. Find the reciprocal of the divisor. Reciprocal of 1/2 is 2/1.
Step 2. Multiply the dividend with the reciprocal: 3×2/1 = 6
3÷1/2 = 6
 Class Notes NCERT Solutions for CBSE Students
Class Notes NCERT Solutions for CBSE Students

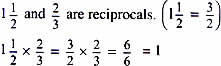




I need worksheet for Class 5th Mathematics.