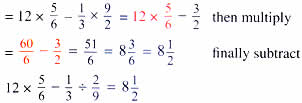Class Notes NCERT Solutions for CBSE Students
(c) 12×5/6-1/3÷2/9
= 12×5/6-1/3÷2/9 first divide
B. Sometimes, we may have an expression using the word ‘of’. You have learnt in fractions how ‘of’ is solved with the help of multiplication. The rule says that ‘of’ has to be solved before division.
So we can add one more operation to our rule for order of operations.
‘Of’ → Division → Multiplication → Addition → Subtraction
48÷2/3 of 72×5
= 48÷2/3 of 72×5 first perform the ‘of’ operation
= 48÷2/3×72×5
= 48÷48×5 = 1×5 then divide
= 1×5 = 5 finally multiply
48÷2/3 of 72×5 = 5
C. Sometimes we have expressions that use brackets. In that case, the brackets are always simplified first.
Brackets → ‘of’ → Division → Multiplication → Addition → Subtraction
Brackets group operations and must be simplified first.
Look at the following examples:
(a) 7+2 × ( 8 – 2 )
= 7 + 2 × ( 8 -2 ) first do the operation within the brackets
= 7 + 2 × 6 next, multiply
= 7 + 12 = 19 finally, add
7 + 2 × (8 – 2) = 19
