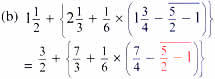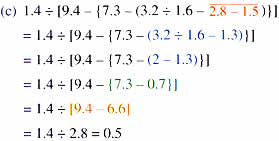Class Notes NCERT Solutions for CBSE Students
(b) 18 + (10 + 2) ÷ 1/3 of 9
= 18 + (10 + 2) ÷ 1/3 of 9 first do the operation within the brackets
= 18 + 12 ÷ 1/3 of 9 = 18 + 12 ÷ 1/3 × 9 next, perform the ‘of’ operation
= 18 + 12 ÷ 3 then do division
= 18 + 4 = 22 finally, add
18 + (10 + 2) ÷ 1/3 of 9 = 22
(c) 7.2 × 1.1 + ( 4.8 – 1.2 )
= 7.2 × 1.1 + ( 4.8 – 1.2 ) first do the operation within the brackets
= 7.2 × 1.1 + 3.6 next, multiply
= 7.92 + 3.6 = 11.52 finally, add
7.2 × 1.1 + ( 4.8 – 1.2 ) = 11.52
D. Different kinds of brackets can be used in an expression. Each has an order in the way they are placed as well as order in which they have to be simplified and removed.
The following list gives the different kinds of brackets starting from the innermost and going to the outermost.
Look at these examples:
= 15 + 8 – ( 7 – 3 ) next, remove the round brackets
= 15 + 8 – 4 Then, add
= 23 – 4 = 19 finally, subtract
Change all mixed numbers to improper fractions and work within the bar
= 3/2 + { 7/3 + 1/6 × ( 7/4 – 3/2) } Remove the bar 5/2 – 1 = 3/2 and work within the round bracket
= 3/2 + { 7/3 + 1/6 × 1/4 } Remove the curved bracket 7/4 – 3/2 = 1/4 and work within the curly bracket
= 3/2 + { 7/3 + 1/24 } Follow BODMAS within curly bracket – multiply 1/6 × 1/4 = 1/24
= 3/2 + 19/8 Remove the curly bracket 7/3 + 1/24 = 57/24 = 19/8
