9th CBSE Mathematics Mid Term Unsolved Paper 2019

9th CBSE Mathematics Mid Term Examination Question Paper (2019-20)

School Name: Himalayan Public School, Sector 13, Rohini, Delhi 110085 India
Time: 3 Hrs.
Marks: 80
Class: 9th
Date: 23/9/2019
Subject: Mathematics

General Instructions:

1. All the questions are compulsory.
2. The question paper consists of 40 questions divided into 5 sections.
3. Section A consists of 16 questions of 1 mark each.
   Section B consists of 3 questions of 2 marks each.
   Section C consists of 8 questions of 3 marks each.
   Section D consists of 6 questions of 4 marks each.
   Section E consists of 7 questions of 3-D Dexture.
4. There is no overall cchoice. However an internal choice has been provided.
5. Use of calculator is not permitted.

9th Mathematics Mid Term: Section A

Fill in the blanks in Q 1 to Q 3

Q 1. There can be _______ many irrational numbers between two numbers on the number line.

Q 2. A polynomial of degree __________ is called constant polynomial.

Q 3. Co-ordinates of a point on the x-axis are of the form ________.

Choose the correct option in Q 4 to Q 6

Q 4. Find the rational number among the following numbers:

1. √64/8
2. √98
3. √98/√2
4. √14

Q 5. The radius of a sphere i 2r, than the volume will be

1. 4/3 πr³
2. 4πr³
3. 8πr³/3
4. 32/3 πr³

Q 6. An exterior angle of a triangle is 105° and its two interior opposite angles are equal. Each of these equal angle is:

1. 37.5°
2. 52.5°
3. 72.5°
4. 75°

Objective type questions (Q 7 to Q 11)

Q 7. Three angles of a quadrilateral are 75°, 90° & 55°, find the fourth angle.

Q 8.  Find the volume of sphere in terms of II whose diameter is 6 cm.

Q 9. Find the length of each side of an equilateral triangle having an area of 9√3 cm².

Q 10. In ΔPQR, PQ = PR and ∠Q = 65°, then find ∠R.

Q 11. Can a triangle have all the angles less than 60°? Give reason.

State whether the following statements are True or False in Q 12 to 16

Q 12. Zero is a rational number.

Q 13. x + 2√x + 1 is  a  polynomial.

Q 14. Two circle of same radii are congruent.

Q 15. Point (0, -7) lies in IV Quadrant.

Q 16. There cannot be more than one obtuse angle in a triangle.

Section B

Q 17. If (x + 1) is a factor of ax³ + 2x + 4a – 9. Find the value of a.

Q 18. Prove that each angle  of an equilateral triangle is 60°.

OR

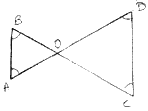
In the given fig.

∠B < ∠A  and ∠C < ∠D

Show that AD<BC

Q 19. The circumference of the base of a cylindrical vessel is 132 cm and its height is 25 cm. How many liters of water can it hold?

Section C

Q 20. Find the value of a and b.

7 + √5 / 7 – √5 – 7 – √5 / 7 + √5 = a + 7/11 √5b

OR

(b) Locate √2 on a number line. [1½]

Q 21. If the polynomial az³ + 4z² + 3z – 4 and z³ – 4z + a leaves the same remainder when divided by z – 3, find the value of a.

OR

Simplify: (a + b + c)² – (a – b – c)² + 4b² – 4c²

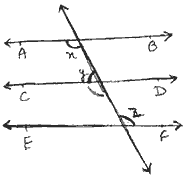
Q 22. In fig. if AB||CD,
CD||EF and y:z = 3:7
Find x

OR
It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP find ∠XYQ and reflex ∠QYP.

Q.23. In figure, AB is a line segment and P is its mid point.
D and E are points on the same side of AB such
that ∠BAD = ∠ABE and ∠EPA = ∠DPB. Show that

1. ΔDAP ≅ ΔEBP
2. AD = BE

Q 24. A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non parallel sides are 14 m and 13 m. Find the area of the field.

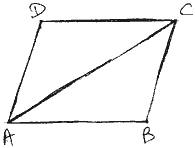
Q.25. In figure, Diagonal AC of a parallelogram
ABCD bisect ∠A. Show that:

1. It bisects ∠C also.
2. ABCD is a rhombus.

OR

Show that the diagonals of a rhombus are perpendicular to each other.

Q 26. Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find

1. radius of base
2. Total surface area of the cone.

Q 27. A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?

9th CBSE Mathematics Mid Term Unsolved Paper 2019: Section D

Q 28. If a = 3 + 2√2, find the value of

Q 29. By actual division, find the quotient and remainder when 3x⁴ – 4x³ – 3x – 1 is divided by x + 1.

OR

If  a + b + c = 6 and and ab + bc + ca = 11, then find the value of a³ + b³ + c³ – 3abc

Q 30. Plot the points A (2,0), B(5,0) and C (5,3). Find the coordinates of the point D such that ABCD is a square. Find the area and perimeter of square.

Q 31.

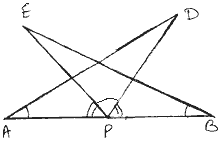
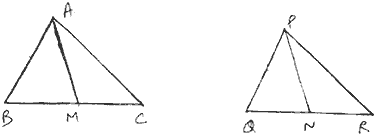
Two side AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and OR and median PN of ΔPQR.
Show that:

1. ΔABM ≅ ΔPQN
2. ΔABC ≅ ΔPQR

OR

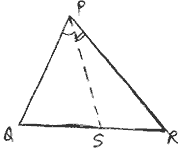
In fig., PR>PQ and PS bisects
∠QPR. Prove that ∠PSR > ∠PSQ.

Q 32. Twenty seven solid iron spheres each of radius r¹ and surface area S are melted to form a sphere with surface area S¹. Find the

1. radius r¹ of the new sphere
2. ratio of S and S¹

OR

Volume of the two spheres are in the ratio 125:27. Find the ratio of their surface areas.

Q 33. ABC is a triangle right angled at C. A line through the mid point M of hypotenuse AB and parallel to BC intersect AC at D. Show that

1. D is the mid point of AC
2. MD⊥AC
3. CM = MA = ½ AB

9th Mathematics Mid Term: Section E (3D – Dexture) [1o]

Fill in the blanks in Q 34 and Q 35

Q 34. ________ 3D Printing technology was invented by Chuck Hull in 1983. [1]

Q 35. _________ 3D Printing technology used in our school. [1]

Choose the Correct option in Q 36 and Q 37

Q 36. Which of the following software we used in 3D printing? [1]

1. Designing software
2. Slicing software
3. None of above
4. both (a) and (b)

Q 37. The name of the material we use for 3D printing is [1]

1. Acrylonitrile Butadirne Styrene
2. Polylactic acid
3. Poly carbonated acid
4. Nylon

Q 38. Give a brief introduction of smart city? [2]

Q 39. What is the difference between alternating current and direct current? What is I.C. and write its full form. [2]

Question: What is the diameter of the filament you use in 3D Printer? What is the full form of FDM? [2]

OR

What is alternating current? From where you obtained AC & DC?