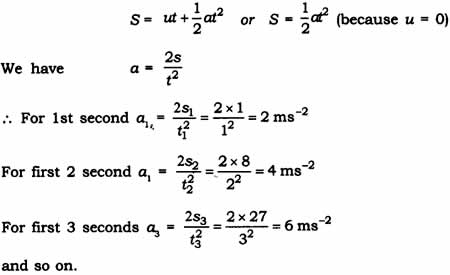Class Notes NCERT Solutions for CBSE Students
Question: A hammer of mass 500 g, moving at 50 ms-1, strikes a nail. The nail stops the hammer in a very short time of 0.01 s. What is the force of the nail on the hammer?
Answer:
Question: The following is the distance-time table on an object in motion:
Time in seconds
Distance in metres
0
0
1
1
2
8
3
27
4
64
5
125
6
216
7
343
(a) What conclusion can you draw about the acceleration? Is it constant, increasing, decreasing, or zero?
(b) What do you infer about the forces acting on the object?
Answer: As per given table initial speed of the object is zero. Applying the relation
Thus it is clear that the acceleration in increasing with time.
Question: A motorcar of mass 1200 kg is moving along a straight line with a uniform velocity of 90 km/h. Its velocity is slowed down to 18 km/h in 4 s by an unbalanced external force. Calculate the acceleration and change in momentum. Also calculate the magnitude of the force required.
Answer:
-ve sign of acceleration, charge in momentum and force suggests that the force is opposing the motion of motor car.
Question: A large truck and a car, both moving with a velocity of magnitude v, have a head- on collision and both of them come to a halt after that. If the collision lasts for 1 s:
(1) Which vehicle experiences the greater force of impact?
(2) Which vehicle experiences the greater change in momentum?
(3) Which vehicle experiences the greater acceleration?
(4) Why is the car likely to suffer more damage than the truck?
Answer:
- During head on collision forces applied by truck and car are action-reaction forces. Hence both vehicles experience same (equal) force of impact.
- Here initial velocity of both car and truck is same equal to v and final velocity of both is zero. But mass of truck is much more than that of car, hence change in momentum of truck is more than change in momentum of car.
- For same force of impact, the acceleration of car will have greater magnitude because its mass is less.
- Car suffers more damage than the truck, as acceleration of car is more, its velocity falls to zero in a shorter time and consequently, its momentum changes in a shorter time.
