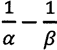10 CBSE Mathematics First Term Exam 2023-24: N.K. Bagrodia Public School, Rohini
| School Name: | N. K. Bagrodia Public School, Sector 9, Rohini, New Delhi 110085 India |
| Class: | 10th Standard (CBSE) |
| Subject: | Mathematics |
| Time Duration: | 03 Hours |
| Maximum Marks: | 80 |
| Date: | ~ September 2023 |
General Instructions:
- This question paper has 5 Sections A – E.
- Section A has 20 MCQs carrying 1 mark each.
- Section B has 5 questions carrying 2 marks each.
- Section C has 6 questions carrying 3 marks each.
- Section D has 4 questions carrying 5 marks each.
- Section E has 3 case based integrated units of assessment (4 marks each) with sub-parts of the values of 1, 1 and 2 marks each respectively.
- All questions are compulsory. However, an internal choice in 2 questions of 5 marks, 2 questions of 3 marks and 2 questions of 2 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
- Draw neat figures wherever required. Take π=22/7 wherever required if not stated.
SECTION- A
Question: 01. If n is any natural number then 2n cannot end with the digit
(a) 0
(b) 2
(c) 4
(d) 8
Question: 02. The number of zeroes of the polynomial f(x) will be
(a) 1
(b) 2
(c) 3
(d) 4
Question: 03. The pair of linear equations 2x = 5y + 6 and 15y = 6x – 18 represents two lines which are:
(a) intersecting
(b) parallel
(c) coincident
(d) either parallel or intersecting
Question: 04. The fifth term of the AP defined by a, = (-1)n. 2n will be
(a) -5
(b) -2
(c) -32
(d) 32
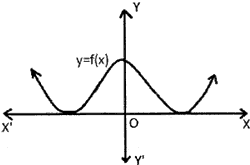
Question: 05. ABC and DEF are two triangles as shown. The measure of ∠F will be
(a) 40°
(b) 60°
(c) 80°
(d) 100°
Question: 06. Evaluate:
![]()
(a) 0
(b) 1
(c) cos²A
(d) cos²A+1
Question: 07. The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is
(a) 22
(b) 24
(c) 24
(d) 75
Question: 08. For the following distribution:

The sum of the lower limits of median class and modal class is
(a) 15
(b) 25
(c) 30
(d) 35
Question: 09. Two numbers are in the ratio 15:11. If their HCF is 13 then the numbers are
(a) 195 and 143
(b) 195 and 133
(c) 185 and 163
(d) 185 and 143
Question: 10. If the zeroes of the quadratic polynomial p(x) = x² + (a+1)x + b are 2 and -3, then the value of ‘a’ will be
(a) – 7
(b) 5
(c) 2
(d) 0
Question: 11. For what value of k, the pair of equations 2x = 5 – 3y and kx + 4y = 10 will have a unique solution?
(a) k = 8/3
(b) k = 3
(c) k ≠ 8/3
(d) k ≠ 3
Question: 12. 30th term of the AP : 10, 7, 4,… is
(a) 97
(b) 77
(c) -77
(d) -87
Question: 13. A vertical pole which is 2.25m long casts a 6.75m long shadow on the ground. At the same time a vertical tower casts a 90m long shadow on the ground. The height of the tower will be
(a) 20m
(b) 30m
(c) 40m
(d) 45m
Question: 14. The length of an arc of a circle of radius 12cm is 107. The central angle of the arc will be
(a) 50°
(b) 100°
(c) 120°
(d)150°
Question: 15. In a given data, if mean and median are 10.5 and 9.6 respectively, then the mode of the data will be
(a) 6.9
(b) 7.8
(c) 12.3
(d) 15.4
Question: 16. If 2sin(3x – 15)° = √3, then the value of x will be
(a) 15°
b) 20°
(c) 25°
(d) 30°
Question: 17. If α and β are the zeroes of g(x) = x2 + x – 2, then the value of
will be

Question: 18. If x = 3 tan²Θ -1 and y = 3 sec²Θ- 6, where Θ is an acute angle, then the value of (x – y) will be
(a) 1
(b) 2
(c) 7
(d) 8
DIRECTIONS: In the question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option out of the following:
Question: 19.
Assertion (A): The point (3,1/3) lies on the line represented by 2x – 3y =5.
Reason (R): Every solution of the linear equation is a point on the graph of the linear equation.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true and Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true birt-R-easm false.
(d) Assertion (A) is false but Reason (R) is true.
Question: 20.
Assertion (A): If S7 = 49, S17 = 289, then Sn = n².
Reason (R): The sum of first n terms is always n².
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true and Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
SECTION – B
Question: 21. If HCF( 198,132) = 11m, find m.
Question: 22. If α and β are the zeroes of the polynomial p(x) = ax²2 – 5x + c where a+/3 = = 10, then find a and c.
OR
If one zero of the quadratic polynomial f(x) = 2×2 – 8x – m is -52 , then find the other zero and m.
Question: 23. Find the 9th term from the end of the AP: 5, 9, 13,…. , 185.
Question: 24. If Θ = 45°, evaluate: 2 sec²Θ + 3 cosec²Θ – 2sinΘcosΘ.
OR
cosA + cos²A = 1, then find sin²A + sin4A.
Question: 25. A car has two wipers which do not overlap. Each wiper has a blade of length 30cm sweeping through an angle of 100°. Find the total area cleaned at each sweep of the blades.
SECTION – C
Question: 26. Find the smallest number which when increased by 12 is exactly divisible by both 168 and 231.
OR
Find the HCF of the polynomials (x2 + 6x+ 9)(x+ 3) and ( x2+ 2x-3) (x- 1).
Question: 27. ABCD is a rectangle (with dimensions in cm) as shown. Find x and y.
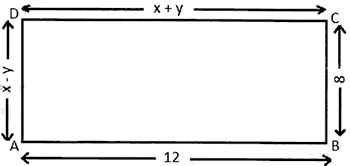
Question: 28. A horse is tied to a rope at one corner of a square shaped grass field of side 20m by means of a 10m long rope. Find the area of the field that horse cannot graze. (use π = 3.14)
Question: 29. In an AP, Sn = n(4n+1). Find the 11th term of this AP.
OR
Solve the equation for x : 1 +4+7+10 +…+x= 287
Question: 30. In the given figure, altitudes AD and CE of ΔABC intersect each other at point P. Show that:
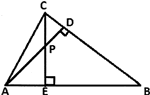
(i) ΔAEP ~ ΔADB
(ii) ΔPDC ~ ΔBEC
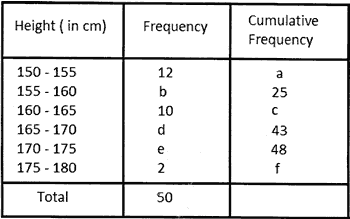
Question: 31. Find the unknown entries a, b, c, d, e, f in the following distribution:
SECTION – D
Question: 32. When 3 is added to the denominator and 2 is subtracted from the numerator a fraction becomes ¼ . And when 6 is added to the numerator and the denominator is multiplied by 3, it becomes ⅔. Find the fraction.
OR
The sum of a two-digit number and the number obtained by reversing the digits is 66. If the digits of the number differ by 2, find the number. How many such numbers are there?
Question: 33. In the given figure, if ΔABE ≅ ΔACD, then show that ΔADE ~ ΔABC
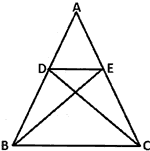
OR
If AD and PM are the medians of triangles ABC and PQR respectively, where ΔABC ~ ΔPQR, then prove that
![]()
Question: 34. (1) Show that
![]()
(2) If
![]()
find A and B.
Question: 35. If the median of the following frequency distribution is 24, then find the missing frequency x:

SECTION – E
Case Study Based questions (10 Mathematics First Term Exam)
Question: 36.
Tunnels are the passages that are meant for transportation. It is a transit constructed below the earth or the water surface. They are constructed to facilitate the transfer of goods, people, sewage, water, cables, etc. Many times some tunnels are constructed for the defense system of the country and they are the secret tunnels.
India holds the honour of having the world’s longest highway tunnel recently constructed in the country and is named as Atal Tunnel.
The figure shows the tunnel whose cross-section is a circle of radius 20m subtending an angle of 90° at the centre 0. A and B are points on the circumference of the circle ancLactas as_hard _ of the circle. M is the mid-point of AB.
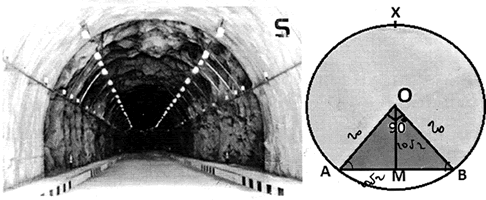
(1) What is the length of the chord AB?
(2) What is the distance of the chord from the centre?
(3) What is the area of the major sector? (n- = 3.14)
OR
(3) What is the perimeter of the major sector? (leave answer in π)
10 Mathematics First Term Exam – Question: 37.
The manager of a Queen Fair must decide what to charge for a ticket to the fair’s toy train rid If the price is too low, then the company would lose money; and if the price is too high, people won’t come. She estimated that the profit P(x) from sales can be approximated by P(x)= – x2 + 220x – 4000, where x is the cost of the ticket.
(1) What is the lowest cost of a ticket that would allow the ride to run without any profit.
(2) What the highest cost of a ticket that would allow the ride to run without any profit.
(3) If the toy train ride charge is 2250 for a ticket, then find out if it would be a profit or loss and of how much?
OR
(3) If the toy train ride charge is 2100 for a ticket, then find out if it would be a profit or loss and of how much?
10 Mathematics First Term Exam – Question: 38.
A grocery store is a food service retail store that primarily retails a general range of food products, which may be fresh or packaged. A grocery store displays cans stacked like a triangle.

The display has 25 cans in the bottom row, 1 can in the top row and each row has two cans less than the row below it.
(1) What is the number of rows in which cans are displayed?
(2) What is the total number of cans in the display?
(3) If the sum of the first two terms of an AP is same as the sum of the first seven terms of the same AP, then find the fifth term of this AP.
OR
(3) Split 207 into three parts such that these are in AP and the product of the two smaller parts is 4623.
 Class Notes NCERT Solutions for CBSE Students
Class Notes NCERT Solutions for CBSE Students