10 CBSE Mathematics Pre-board Exam 2023-24: N.K. Bagrodia

10 Mathematics Pre-board Exam 2023-24: N.K. Bagrodia Public School, Rohini

School Name:	N. K. Bagrodia Public School, Sector 9, Rohini, New Delhi 110085 India
Class:	10th Standard (CBSE)
Subject:	Mathematics Standard
Time Duration:	03 Hours
Maximum Marks:	80
Date:	~ December 2023 – January 2024

General Instructions:

1. This question paper has 5 Sections.
2. Section A has 20 MCQs carrying 1 mark each.
3. Section B has 5 questions carrying 2 marks each.
4. Section C has 6 questions carrying 3 marks each.
5. Section D has 4 questions carrying 5 marks each.
6. Section E has 3 case-based integrated units of assessment (4 marks each) with sub-parts of the values of 1, 1 and 2 marks each respectively.
7. All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks, and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2-mark questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

SECTION – A

Question 01.

The HCF of k and 93 is 31, where k is a natural number. Which of these can be true for some values of k?

1. K is a multiple of 31.
2. K is a multiple of 93.
3. K is an even number.
4. K is an odd number.

a) Only 2 and 3
b) Only 1, 2, and 3
c) Only 1, 3 and 4
d) All are true

Question 02. Which of the following are polynomials?

(i) √3 x+ 1/x
(ii) 2  + 3x²
(ii) 1/ (x² + 4x + 6)
(iv) -3/x + 2x²

a) (i), (ii) and (iii)
b) (ii), (iii), and (iv)
c) (i) and (iv)
d) None of these

Question 03. Geometrical representation of a linear equation is

a) a circle
b) a point
c) a straight line
d) None of these as a linear equation can’t be expressed geometrically.

Question 04.

The number of real roots of the equation
(x -1)² + (x +1)² + (x -2)² = 0 is

a) 0
b) 1
c) 2
d) 3

Question 05.

Three numbers are in A.P. having sum 24. Its middle term is

a) 2
b) 4
c) 8
d) 12

Question 06. In the given figure,

DE II AB, AD = 2x, DC = x + 3, BE = 2x – 1 and CE = x. The value of x is

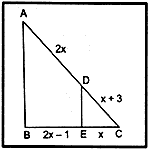
a) 5/3
b) 3/5
c) 3/2
d) 2/3

Question 07.

The coordinates of one end point of a diameter of a circle are (4,-1) and the coordinates of the centre are (1,-3). Then the coordinates of the other end of the diameter are

a) (-2,5)
b) (2,5)
c) (-5,-2)
d) (-2,-5)

Question 08. 

If Cos y = 0, then the value of (Cos y/2)/2 is

a) 0
b) √2
c) 1/√2
d)1/2√2

Question 09.

In the adjacent figure, PQ is the common tangent to both the circles, SR and PT are also tangents as shown in the figure. If SR = 4 cm and PT = 7cm, then the value of RP is

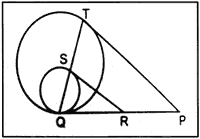
a) 3 cm
b) 4 cm
c) 5 cm
d) 4/√2

Question 10.

The class mark of the modal class in the following frequency distribution is

a) 22
b) 22.5
c) 12
d) 27.5

Question 11.

For an event E, P(E) + P (not E) = x, then the value of x² – 3 is

a) -2
b) -1
c) 1
d) 2

Question 12.

A sphere of maximum volume is cut out from a solid hemisphere of radius 7cm. What is the ratio of the volume of the hemisphere to that of the cut-out sphere?

a) 2:1
b) 3:1
c) 4:1
d) None of them

Question 13.

The radius of a circle is 50 cm. If the radius is decreased by 50%, its area will be decreased by

a) 25%
b) 50%
c) 75%
d) 80%

Question 14.

If x =k√2 is a solution of the quadratic equation x2+√2x – 4 = 0 then the value of k is

a) -1
b) -2
c) 2
d) 4

Question 15.

If 3x = Cosecθ and 3/x = Cotθ, then the value of 3(x² -1/x²) is

a) 1/9
b) 9
c) 1/3
d) 3

Question 16.

The perimeter of a A with vertices (0,4), (0,0) and (3,0) is

a) 5 units
b) 12 units
c) 11 units
d) (7 + √5) units

Question 17.

AT is a tangent to a circle with centre 0. A is the-point of contact. OT = 4 cm and LOTA = 30°, Then AT is equal to

a) 4 cm
b) 2 cm
c) 2√3 cm
d) 4√3 cm

Question 18.

In the figure, O is the centre of the circle. The shaded sector has an angle of 280° and area ‘a’ cm². Which of the following is the area of the unshaded region?

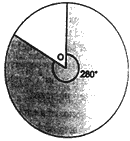
a) 2a/7 cm²
b) a/3 cm²
c) 7a/9 cm²
d) 2a/3 cm²

Question 19.

Assertion: Let the positive numbers a, b, c are in AP, then 1/bc, 1/ac, 1/ab are also in AP.

Reason: If each term of the AP a, b, c is divided by abc, then the resulting sequence is also in AP.

a) Both A and R are true and R is the correct explanation of A
b) Both A and R are true but R is not the correct explanation of A
c) A is false but R is true
d) Both A and R are false

Question 20.

Assertion: The CSA of a cone of base radius 6cm and slant height 10 cm is 60π cm².

Reason: The CSA of a right circular cone is πr(l+r) where ‘r’ is the radius and ‘I’ is the slant height of the cone.

a) Both A and R are true and R is the correct explanation of A
b) Both A and R are true but R is not the correct explanation of A
c) A is true but R is false
d) A is false but R is true

SECTION – B

Question 21.

If 7 Cos²θ + 3 Sin²θ = 4, then find the value of tanθ.

OR

Find the value of (1 + tanθ + Secθ)(1+ Cotθ – Cosecθ).

Question 22.

Find the area of the triangle bounded by two lines and x = 0 in the adjacent graph.

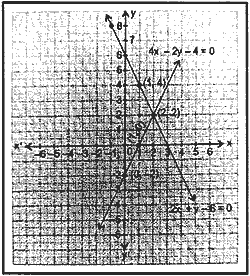
Question 23.

In ∆ABC, LA is obtuse, PB L AC and QC ± AB. Prove that AB x AQ = AC x AP.

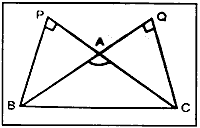
Question 24.

Volumes of two spheres are in the ratio 64:27. Find the ratio of their total surface areas.

Question 25.

A three digit number is chosen. Find the probability at all three digits are not same.

OR

There are 1000 sealed envelopes in a box, 10 of them contain a cash prize of ₹100 each, 100 of them contain a cash prize of ₹50 each and 200 of them contain a cash prize of ₹10 each. Rest do not contain any cash prize. If they are well shuffled and one envelope is then picked out, what is the probability that it is empty.

SECTION-C

Question 26.

Prove that (1 + 1/√5)² is an Irrational number.

Question 27.

If one zero of the polynomial p(x) = (a²+4) x² + 13x + 4a is the reciprocal of the other, find a.

Question 28.

A plane left 30 minutes later than the schedule time and in order to reach its destination 1500 km away in time, it has to increase its speed by 250 km/hr from its usual speed. Find its usual speed.

OR

A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km / hr less, then it would have taken 3 hours more to cover the same distance. Find the speed of the train.

Question 29.

In the figure, DE || OQ and DF || OR. Show that EF || QR.

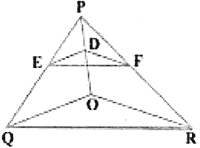
OR

If one diagonal of a trapezium divides the other diagonal in the ratio 1:3. Prove that one of the parallel sides is three times the other.

Question 30. 

From the top of a cliff 25m high, if the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower, then find the height of the tower.

Question 31.

A die is thrown twice. What is the probability that a) 5 will not come up either time?

a) 5 will not come up either time?
b) a product of 11 appears?

SECTION – D

Question 32.

Divide 48 into 4 parts which are in AP such that the ratio of product of extremes V to the product of means of the terms is 27:35.

OR

An AP consists of 37 terms. The sum of the three middle most terms is 225 and the sum of the last three terms is 429. Find the AP.

Question 33.

A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are given only to persons having age 18 years onwards but less than 60 years.

Question 34.

a) If A (-2,1), B(a,0), C (4, b) and D (1,2) are the vertices of a parallelogram. Find the values of a and b. (2)

b) The line segment joining the points A (2,1) and B (5, -8) is trisected at the points P and Q such that is nearer to A. If P also lies on the line given by 2x – y + k = 0, find the value of k. (3)

Question 35.

Sides of a triangular field are 15 m, 16 m and 17 m. At the three corners of the field, a cow, a buffalo and a horse are tied separately with ropes of 7 m each to graze in the field. Find the area of the field which cannot be grazed.

OR

In the figure, ABC is a quadrant of a circle of radius 14 cm, and a semicircle is drawn with BC as a diameter. Find the area of the shaded region.

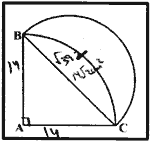
SECTION – E

Case study-based questions: 

Question 36.

As a part of Gender Sensitisation Campaign, a huge spherical Balloon with the message “SAVE GIRL CHILD” is displayed from the terrace of a building. The balloon is held by strings of length 9m each which are inclined at an angle of 60° at the point where it is tied, as shown in the figure.

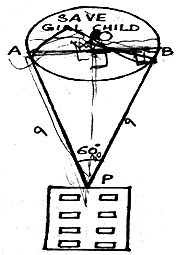
Answer the following questions based on it:

a) Assume O to be the centre of the balloon, find LOBA.
b) Find the length of chord AB.
c) Find the radius of the balloon.

OR

c) Which type of quadrilateral is OAPB? Justify your answer.

Question 37.

The figure shows a wax candle in the shape of a right circular cone with base radius 7 cm and height 12cm. It takes 1 hour 40 minutes to burn it completely.

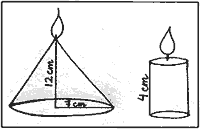
Answer the following questions based on it:

a) Find the volume of the wax used for making the candle. (1)
b) If the candle is burning at a constant rate, then find the height of the remaining candle after 25 minutes. (1)
c) If 1/4 of the volume of the melted wax is poured into a cylindrical mould to make a new cylindrical wax candle with height 4cm, then find the radius of the new candle. (2)

OR

c) Find the ratio of the height of the conical candle left after burning for 50 minutes to the height of the original candle.

Question 38.

The greatest epic of all times, Mahabharata has given us enough lessons about life which is applicable in today’s time as well. Once, Dronacharya, the teacher of Pandavas and Kauravas, placed a wooden bird on a branch and asked all students to aim at the eye of the bird. Among all, Arjun concentrated only on his target and replied “I can only see the eye of the bird.” Based on the same concept a Mathematics teacher designed the following question.

A spherical balloon of radius 3 cm subtends an angle of 60° at the eye of an observer. The angle of elevation of the centre of the balloon is 45′.

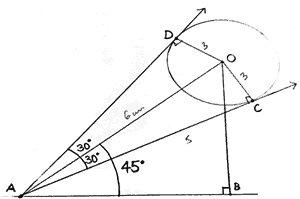
Answer the following questions based on it:

a) Find the angle subtended by radii at the centre O. (1)
b) Find the length of the line segment OA. (1)
c) Find the area of AOCA. (2)

OR

c) Find the height of the centre of the balloon. (2)