10 Class Maths Periodic Test III (2018-19)

10th Mathematics Periodic Test III (2018-19)

School Name: Venkateshwar Global School, Sector 13, Rohini, Delhi 110085 India
Time: 3 hours
M.M: 80
Subject Code: 041
Class: X
Subject: Mathematics
Date: 21.01.2019

General Instructions:

• All questions are compulsory.
• The question paper consist of 30 questions divided into four section A, B, C, and D. Section A comprise of 6 questions of 1 mark each, Section B comprises of 6 questions of 2 marks each, Section C comprises of 10 questions of of 3 marks each and Section D comprises of 8 questions of 4 marks each.
• Use of calculator is not permitted.

Section A

Question: 1. The nth term an AP is 7 – 4n. Find its common difference.

Question: 2. What is the HCF of smallest prime number and the smallest composite number?

Question: 3. Find the distance of the point (-8, 6) from the origin.

Question: 4. Write the polynomial whose zeroes are 2 +√3 and 2 – √3.
OR
If (x + a) is a factor of 2x² + 2ax + 5x + 10 = 0, then find the value of a.

Question: 5. Find the value of cos²67° – sin²23°.
OR
If tanθ = cot (30° + θ), find the value of θ.

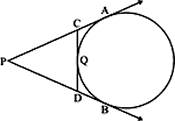
Question: 6. In the given figure, PA and PB are tangents to the circle. CD is a third tangent touching the circle at Q. If PB = 10 cm and CQ = 2cm, what is the length of PC?

Section B

Question: 7. A bag contains 5 red, 8 green and 7 white balls. One ball is drawn at random from the bag. Find the probability of getting:
(a) A white ball or green ball          (b) Neither a green ball nor a red ball.

Question: 8. Determine the value of m and n, so that the following system of linear equations has infinite number of solutions:
(2m – 1)x + 3y – 5 = 0
3x + (n – 1)y – 2 = 0

Question: 9. Show that the square of any positive integer is of the form 3m or 3m + 1 for some integer m.
OR
Prove that 8+9√7 is an irrational number, given that √7 is irrational.

Question: 10. If the distances of P(x,y) from the points A(3,6) and B(-3,4) are equal, prove that 3x + y = 5.

Question: 11. A game consists of tossing a one-rupee coin three times and nothing its outcome each time. Find the probability of getting
(a) atleast two tails        (b) three heads

Question: 12. How many terms of the AP 18, 16, 14…. should be taken so that their sum is zero?
OR
Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.

Section C

Question: 13. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.

Question:14. If 4tanθ = 3, evaluate 4sinθ – cosθ + 1/4sinθ + cosθ – 1
OR
If tan(A+B) = √3 and tan(A-B) – 1/√3, find A and B.

Question: 15. Size of agriculture holding in a survey of 200 families is given in the following table:

Computer the mode size of holding.

Question: 16. If the area of two similar triangles are equal, prove that they are congruent.
OR
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of the diagonals.

Question: 17. A merchant has 120 litres of oil of one kind, 180 litres of another kinds and 240 litres of third kind. He wants to sell the oil by filling the three kinds of oil in tins of equal capacity. Using Euclid’s lemma, determine the greatest capacity of such a tin.

Question: 18. If α and β are the zeroes of the quadratic polynomial p(x) = 6x² – 7x – 3, then form a  quadratic polynomial whose zeroes are 1/α and 1/β.

Question: 19. Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2,3).
OR
Find the coordinates of the points of trisection of the line segment joining the points P(2,-2) and Q(-7, 4)

Question: 20. A well of diameter 3 m is dug 14 m deep. The earth taken out if it has been spread evenly all around it in the shape of s circular ring of width 4 m to form an embankment. Find the height of the embankment.
OR
A container opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the area of metal sheet used to make the container.

Question: 21. In the adjoining figure, O is the centre of a circle with diameter 25 cm. Also, AC = 24cm, AB = 7cm and ∠BOD = 90°. Find the area of the shaded region. (use π = 3. 14)

Question: 22. A place left 30 minutes late than its scheduled time and in order to reach the destination 1500 km away in time, it had to increase its speed by 100 km/h from the usual speed. Find its usual speed.

Section D

Question. 23. From the top of a tower 100 m high, a man observe two cars on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the cars. (use √3 = 1.73)

OR

The angle of elevation of a cloud from a point 50 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud above lake level.

Question: 24. 

Question: 25. Construct a tangent to a circle of radius 4cm from a point on the concentric circle of radius 6cm.

Question: 26. If the median of the distribution given below is 28.5, find the value of x and y.

Question: 27. State and prove the Pythagoras theorem.

Question: 28. A vessel in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one – fourth of the water flows out. Find the number of lead shots dropped in the vessel.

Question: 29. 2 men and 5 boys can finish a piece of work in 4 days while 3 men and 6 boys can finish the work.

OR

Two years ago, a father was five time as old as his son. Two years later, his age will be 8 more than three times the age of the son. Find the present ages of father and son.

Question: 30. The sum of first six terms of an arithmetic progression is 42. The ratio of its 10th term to its 30th term is 1:3. Calculate the first and thirteenth term of the AP.