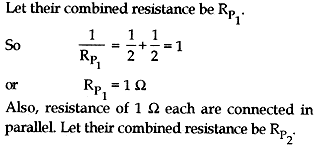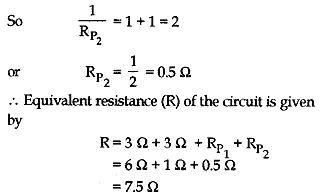Electricity: 10th CBSE Science Physics

Question: A hot plate of an electric oven connected to a 220 V line has two resistors A and B each of 22 Ω resistance. These resistors a my be used separately, in series or in parallel. Find the current flowing in all the three cases.

Answer:

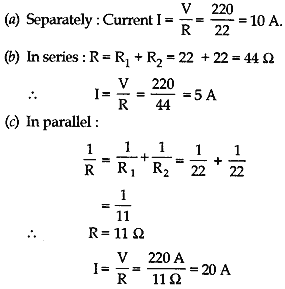
Question: Find the equivalent resistance of the following circuit:

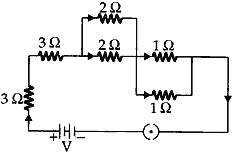
Answer: Resistances of a 2Ω each are connected in parallel.

Question: Two lamps, one is rated 100 W at 220 V, and the other 60 W at 220 V, are connected in parallel to a 220 V supply. Find the current drawn from the supply line.

Answer:

Resistance of first lamp = R₁
Resistance of second lamp = R₂
We know that

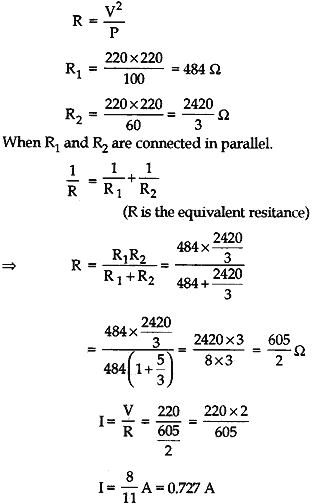
Question: An electric kettle of 2 kW works for 2 h daily. Calculate the (a) energy consumed in SI and commercial units (b) cost of running it in the month of June at the rate of Rs. 3.00 per unit.

Answer:

1. Here, power, P = 2 kW = 2000 W, time, t = 2h
   Energy, E = P×t = 2000 W × 2 h = 4 kWh
2. Total energy consumed in June
   = 4 × 30 kWh
   = 120 kWh
   ∴ Total cost = 120 × 3.00 = Rs. 360

Question: Two bulbs A and B are rated as 90 W – 120 V and 60 W – 120 V respectively. They are connected in parallel across a 120 V source. Find the current in each bulb. Which bulb will consume more energy?

Answer: (i) For the first bulb,

(ii) Bulb A will consume more energy, because it has more power.

Question: A wire connected to a bulb does not glow, whereas the filament of the bulb glows when the same current is passed through them. Why?

Answer: Filament of the bulb and the supply lines are connected in series. So the same current flows through them. Since the resistance of the connecting wires is negligibly small as compared to the resistance of the filament and heat produced is directly proportional to the resistance, therefore, the heat produced in the filament is more. Hence, the bulb glows, but the connecting wires remain practically unheated.

Question: Derive the relation R = R₁+ R₂+ R₃ when three resistors R₁, R₂, R₃ are connected in series in an electric circuit.

Answer: Consider three resistors of resistances R₁, R₂ and R₃ connected in figure. Since the three resistors are connected in series, therefore, the current I through each of them is same.

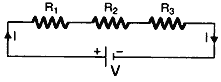
Then by Ohm’s law, the potential drop across each resistor is given by
_V1 = IR₁, V₂ = IR₂ and V₃ = IR₃.
Since V is the total potential in the circuit, therefore, by conservation of energy, we have
V = V₁ + V₂ + V₃  … (1)
Substituting for V₁, V₂ and V₃ in equation (1), we have
V = IR₁ + IR₂ + IR₃  … (2)
If R_s is the equivalent resistance of the series combination, then by Ohm’s law, we have
V = IR_s  … (3)
Therefore, from equations (2) and (3), we have
IR_s = IR₁ + IR₂ + IR₃
Hence, R_s = R₁ + R₂ + R₃  … (4)

Thus, in series combination, the equivalent resistance is the sum of the individual resistances.

Question: Derive an expression for equivalent resistance when three resistors of resistance R₁ , R₂ and R₃ are connected in parallel.

Answer: Consider three resistors R₁, R₂ and R₃ are connected in parallel as shown in figure.

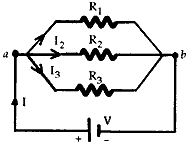
When the current I reaches point ‘a’, it splits into three parts I₁ going through R₁, I₂ going through R₂ and I₃ going through R₃. The current will tend to take the path of least resistance.

Since charge must be conserved, therefore, the current I that enters point ‘a’ must be equal to the current that leaves that point. Therefore, we have
I = I₁ + I₂ + I₃ … (1)
Since the resistors are connected in parallel therefore, the potential difference across each must be same, hence by Ohm’s law, we have

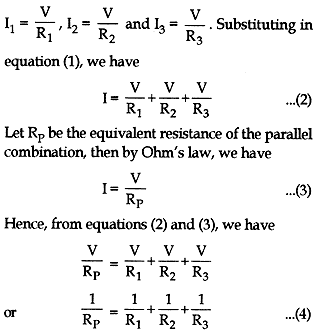
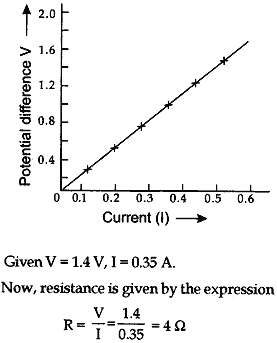
Question: State the formula co-relating the electric current flowing in a conductor and the voltage applied across it. Also, show this relationship by drawing a graph. What would be the resistance of a conductor, if the current flowing through it is 0.35 ampere when the potential difference across it is 1.4 volt?

Answer: It states that “Physical conditions remaining same the current following through a conductor is directly proportional to the potential applied across its two ends.”

The graph is as shown below:

Question: (1). Define the term ‘volt’.
(2). State the relation between work, charge and potential different for an electric circuit. Calculate the potential difference between the two terminals of a battery, if 100 joules of work is required to transfer 20 coulombs of charge from one terminal of the battery to the other.

Answer:

1. One volt is the potential difference between two points in a current carrying conductor when 1 joule of work is done to move a charge of 1 coulomb from one point to the other.
2. The relation is V = W/Q
   Give W = 100 J, Q = 20, V = ?
   Using the relation V = W/Q, we have
   V = 100/20 = 5 V